Sistema de ecuaciones

Sistema de ecuaciones

En las matemáticas, un sistema de ecuaciones es un conjunto de dos o más ecuaciones con varias incógnitas. Una solución para el sistema debe proporcionar un valor para cada incógnita, de manera que en ninguna de las ecuaciones del sistema se llegue a una contradicción. En otras palabras el valor que reemplazamos en las incógnitas debe hacer cumplir la igualdad del sistema.
Las incógnitas se suelen representar utilizando las últimas letras del alfabeto latino, o si son demasiadas, con subíndices.
Sistema general
La forma genérica de un sistema de ecuaciones y incógnitas es la siguiente:
(1)
donde son funciones de las incógnitas. La solución, perteneciente al espacio euclídeo , será tal que el resultado de evaluar cualquier expresión con los valores de dicha solución, verifique la ecuación.
Representación gráfica
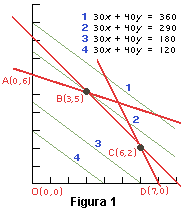
Los sistemas de 2 o 3 incógnitas admiten representaciones gráficas cuando las funciones en (1) son continuas a tramos. En cada ecuación se representa como una curva o una superficie curva. La existencia de soluciones en ese caso puede deducirse a partir de la existencia de intersecciones comunes a dichas curvas o superficies curvas.
Clasificación de los sistemas
Un sistema de ecuaciones sobre puede clasificarse de acuerdo con el número de soluciones en:
Sistema incompatible cuando no admite ninguna solución.
Sistema compatible cuando admite alguna solución que a su vez pueden dividirse en:
Sistemas compatibles indeterminados cuando existe un número infinito de soluciones que forman una variedad continua.
Sistemas compatibles determinados cuando admiten un conjunto finito de soluciones, o un conjunto infinito de soluciones aisladas con a lo sumo un número finito de puntos de acumulación.
Sistema lineal
Un sistema como el anterior en que las anteriores ecuaciones son funciones afines. A diferencia del caso general, la solución de los sistemas de ecuaciones lineales son fáciles de encontrar cuando los coeficientes de las ecuaciones son números reales o complejos. También existen medios generales cuando los coeficientes pertenecen a un anillo, aunque la búsqueda de las soluciones en ese caso puede ser un poco más complicada.
Una característica importante de los sistemas lineales de ecuaciones es que admiten la llamada forma matricial. Esa forma permite representar el sistema usando tres matrices, de la siguiente forma:
(2)
La primera es la matriz de coeficientes, donde el término representa al coeficiente que acompaña a la j-ésima incógnita de la ecuación i-ésima. La segunda es la matriz de incógnitas, donde cada término se corresponde con una de las incógnitas que queremos averiguar. Y la tercera matriz es la de términos independientes, donde el cada representa al término independiente de la ecuación i-ésima.
Esta representación matricial facilita el uso de algunos métodos de resolución, como el método de Gauss, en el que, partiendo de la matriz aumentada (matriz de coeficientes a la que se le ha acoplado la matriz de términos independientes), y aplicando transformaciones lineales sobre las ecuaciones, pretendemos llegar a una matriz de este tipo:
Una vez la matriz se ha triangulado, el valor de cada término se corresponderá con el de la incógnita . Si nos encontramos alguna fila del tipo , con , el sistema no tendrá solución.
Existencia de soluciones
El teorema de la función inversa proporciona condiciones suficientes de existencia de solución, de un sistema como (1) con . Si sucede que la función vectorial:
Es diferenciable con continuidad, es decir, es de clase y su jacobiano no se anula en ningún punto entonces existe una única solución del sistema (1). Ya que en ese caso existirá una función inversa, y podremos escribir la solución buscada simplemente como:
Sin embargo, la condición de diferenciabilidad anterior aún siendo condición suficiente, no es una condición necesaria, por lo que existen sistemas de ecuaciones en que las funciones no son diferenciables y sin embargo, existen soluciones. Más aún, en casos en que existe más de una solución si la función es diferenciable entonces el jacobiano se anula en algún punto, pero eso no impide que existan varias soluciones.
En casos de un menor número de ecuaciones que de incógnitas, cuando , entonces el sistema es complatible indeterminado o carece de soluciones. En esos casos, el teorema de la función implícita proporciona condiciones suficientes, aunque no necesarias, para la existencia de soluciones de un modo similar a como el teorema de la función inversa las proporciona en el caso .
Método de Gauss-Jordan:
El método de Gauss-Jordan utiliza operaciones con matrices para resolver sistemas de ecuaciones de n número de variables.
Para aplicar este método solo hay que recordar que cada operación que se realice se aplicara a toda la fila o a toda la columna en su caso. Procedimiento:
Primero se debe tener ya el sistema de ecuaciones que se quiere resolver y que puede ser de n numero de variables por ejemplo:
-3x+3y+2z=1 4x+y-z=2 x-2y+z=3
Y se acomodan los coeficientes y los resultados en una matriz:
El objetivo de este método es tratar de convertir la parte de la matriz donde están los coeficientes de las variables en una matriz identidad que es una matriz con puros 0 y 1 pero los 1 están en diagonal así:
Esto se logra mediante simples operaciones de suma, resta y multiplicación. Entonces, si se quiere convertir la primera matriz en la segunda, se puede observar que el -3 de la primera matriz se tiene que convertir en un 1, según la matriz identidad, así que hay que dividir entre -3, pero como una operación se aplica a toda la fila, entonces toda la primera fila se tiene que dividir entre -3 y queda más o menos así:
Después, como se ve en la matriz identidad, hay que hacer 0 toda la columna debajo del 1, y se hace multiplicando por algo la fila de arriba y sumándola a la fila de abajo, en este caso, si se multiplica por -4 la fila de arriba, la primera multiplicación es -4x1, que sumado a la primera coordenada de la fila de abajo da el 0 que se desea, igualmente, la operación se realiza con toda la fila por lo que a cada posición de la fila de arriba se le multiplica por -4 y se suma con la correspondiente posición de la fila de abajo. La siguiente multiplicación seria -4x-1 y se sumaría con el 1 de abajo. La matriz va quedando de la siguiente manera:
En la imagen de al lado ya se termino de hacer 0 las posiciones que se requieren según lo indica la matriz identidad. (Las R son por Row en ingles)
El siguiente paso para lograr una matriz identidad es obtener el siguiente 1, que en este caso iría en donde está el 5 en la segunda fila. Como ya se trabajo con la primera columna ya no es necesario tomarla en cuenta puesto que se supone que ya está bien. Para lograr un 1, hay que dividir toda la segunda fila (sin tomar en cuenta la primera columna) entre 5 y la matriz queda así:
Después se tienen que hacer 0 los que están arriba y abajo del 1, que en este caso seria, para el que está arriba 1xR2+R1 porque el R1 es un -1 y al sumarse con el 1 que da de la multiplicación de 1xR2 da el 0 que se está buscando. De igual manera para el que está debajo es el mismo procedimiento porque en este ejemplo coincidió que los 2 fueran -1, pero hay que recordar siempre buscar el numero por el cual multiplicar para que a la hora de sumar de un 0.
Una vez que se obtuvieron los 0 solo falta obtener el ultimo 1 según la matriz identidad. Esto se logra dividiendo entre 2 toda la tercera fila ignorando ya los que fueron hechos ceros.
La matriz queda de la siguiente manera:
Por último solo se hacen 0 los que están encima del que acabamos de hacer 1, en este caso multiplicando por 1/3xR3 y sumándola a R1 para hacer el 0 que se necesita, y multiplicando -1/3xR3 y sumándolo a R2 para obtener el ultimo 0:
Como se podrá notar, una matriz identidad siempre es cuadrada y al pasarla a nuestra matriz original sobro la columna donde iban los resultados de cada ecuación, pues bien, esa última columna contiene los valores de las variables que se están buscando y en orden, la de arriba es la primer variable, la de en medio es la segunda y la última es la tercera.

Método Simplex

El Método Simplex publicado por George Dantzig en 1947 consiste en un algoritmo iterativo que secuencialmente a través de iteraciones se va aproximando al óptimo del problema de Programación Lineal en caso de existir esta última.
El Método Simplex hace uso de la propiedad de que la solución óptima de un problema de Programación Lineal se encuentra en un vértice o frontera del dominio de puntos factibles (esto último en casos muy especiales), por lo cual, la búsqueda secuencial del algoritmo se basa en la evaluación progresiva de estos vértices hasta encontrar el óptimo. Cabe destacar que para aplicar el Método Simplex a un modelo lineal, este debe estar en un formato especial conocido como formato estándar el cual definiremos a continuación.