Resolución gráfica de problemas

Resolución gráfica de problemas

Consideremos el siguiente problema a resolver gráficamente:
Max z = 3x1 + 5x2
sa: x1 £ 4
3x1 + 2x2 £ 18
x1,x2 ³ 0
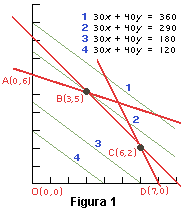
En primer lugar, se debe obtener la región de puntos factibles en el plano, obtenida por medio de la intersección de todos los semi - espacios que determinan cada una de las inecuaciones presentes en las restricciones del problema.
Enseguida, con el desplazamiento de las curvas de nivel de la función objetivo en la dirección de crecimiento de la función (que corresponde a la dirección del vector gradiente de la función, z(x1,x2) = (3,5)T), se obtiene la solución óptima del problema en la intersección de las rectas: 2x2 = 12 y 3x1+2x2 = 18 (restricciones activas). Esto es:
x1* = 2 x2* = 6
z* = 3 x1* + 5 x2* = 36
Notar que se pueden dar otras situaciones en la búsqueda de una solución óptima para esta clase de problemas:
1) La solución óptima exista pero haya más de una. En el ejemplo, considere la nueva función objetivo: z = 6x1+4x2.
2) El problema no tenga solución, dada una región de puntos factibles no - acotada. En el ejemplo, reemplace cada desigualdad  por una .
3) El problema no tenga solución, porque no existen puntos factibles. En el ejemplo, suponga que agregamos la restricción: x1  5.